Most distributed databases rely on a timestamp oracle to order events. In our case, we have a service called TimeOracle that uses a distributed lock to ensure monotonic timestamps. However, it can’t avoid brief periods of unavailability. TaaS proposes a timestamp service that could serve as a perfect replacement for TimeOracle. I became curious about how to maintain monotonic timestamps while avoiding unavailability—so let’s dive into it.
Paper Link #
Timestamp as a Service, not an Oracle
Terminology #
- session: A session starts when the client requests a timestamp, and ends when all the servers reply.
- \(N\) : The number of servers.
It provides #
- Availability that the timestamps are always computable, provided any majority of the server clocks being observable.
- Correctness that all the computed timestamps must increase monotonically over time, even if some clocks become unobservable.
Algorithm #
A client starts a session by broadcasting a timestamp (⊥) to all servers. In basic scenarios, ⊥ can be looked as negative infinity.
Each server has a persistent timestamp \(c\) . When it receives a request, it increments its timestamp and returns the new value (noted as \(c \oplus t\) ) to the client. The new value can be \(max(c, ⊥) + 1\) . This means that the client always knows that before it requested to the server, the server had a timestamp less than the timestamp it just received from the server.
After the session is completed, the client uses the \(M^{th}\) ‑smallest timestamp from the replies, where \(M \lt N\) and \(M\) is shared by all clients. (The best practice says that \(M\) should be the smallest majoriy, even though \(M\) can be anything between 1 and \(N\) )
Definition
The timestamp for session \(T\) is guaranteed larger than the timestamp for any session \(S\) that ended before \(T\) began.
Assumes no server failures or message loss, here comes the basic correctness proof.
basic correctness proof
- The \(M^{th}\) ‑smallest response in \(S \le\) the \(M^{th}\) ‑smallest server state at the end of \(S\) . (Servers’ timestamps increase monotonically.)
- The \(M^{th}\) ‑smallest server state at the end of \(S \le\) the \(M^{th}\) ‑smallest server state at the start of \(T\) . (Monotonicity, and \(S\) ends before \(T\) starts.)
- The \(M^{th}\) ‑smallest server state at the start of \(T \lt\) the \(M^{th}\) ‑smallest response in \(T\) . (The client makes all the servers increment their timestamps during \(T\) .)
- By transitivity, the \(M^{th}\) ‑smallest response \(\lt\) the \(M^{th}\) ‑smallest response in \(T\) .
If servers can crash, then things become a bit more complicated. Let’s look back at the definition. There are two facts that the definition above depends on:
- \(t \gt M^{th}\) ‑smallest of all servers’ timestamps when the session started
- \(t \le M^{th}\) ‑smallest of all servers’ timestamps when the session ends
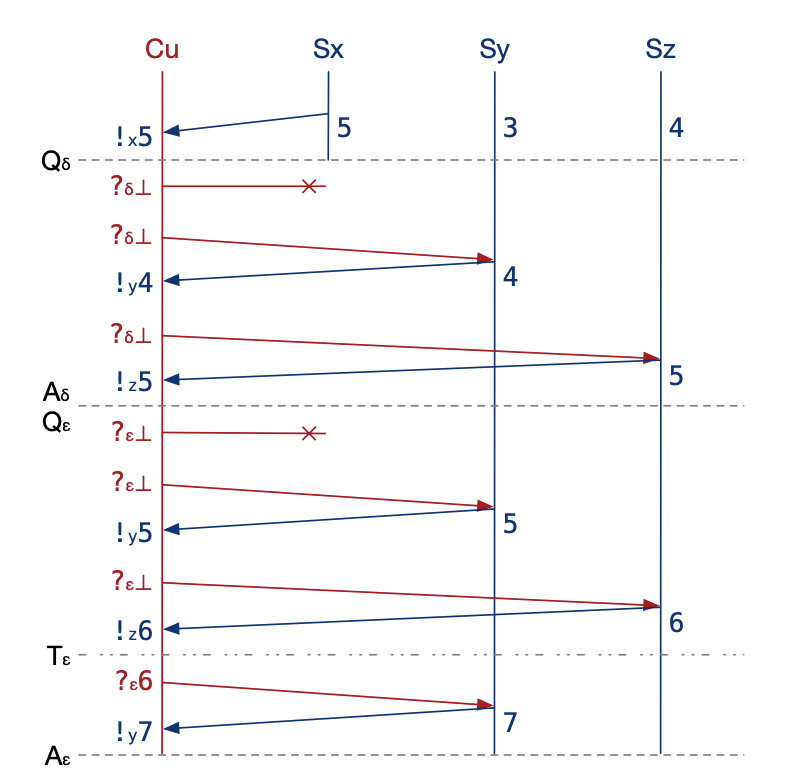
Let’s look at the example from the paper, where M is 2:
In session δ, the client remember that it got the timestamp 5 in some past session from Server X. Therefore it can pick 5 because the clients knows:
- \(5 \gt 2^{th}\) ‑smallest of all servers’ timestamps when the session started: The client heard Servers Y and Z respond with timestamps 4 and 5, so their previous timestamps were less than 5.
- \(5 \le 2^{th}\) ‑smallest of all servers’ timestamps when the session ends: The client knows Servers X and Z now have timestamps at least 5.
Depends on these two facts, the definition is true. However in session ε, the client doesn’t know the second-smallest timestamp. Thus, both of these scenarios may be true:
- X is 7, then the second‑smallest would be 6.
- X is 5.5, then second‑smallest would be 5.5.
How to solve this problem? The client continues this session, and sends 6 to Server Y.
- Why 6? Because it thinks 6 might be the second-smallest timestamp.
- Why Server Y? It got 5 from the Server Y, so Server Y might have the timestamp less than 6.
Now the Server Y updates its own timestamp to at least 6. Let’s assume it is 7, so the client has 6 from Z, 7 from Y. Then:
- \(6 \gt 2^{th}\) ‑smallest of all servers’ timestamps when the session started: The first trip the client received from Y and Z with 5 and 6, so they started session with less than 6.
- \(6 \le 2^{th}\) ‑smallest of all servers’ timestamps when the session ends: The second trip the client reveived from Y and Z with 7 and 6, they ended with at least 6.
With one more trip, the client achieved certainty.
How to keep unique timestamps?
Annotate each timestamp with its sending server’s identifier. Timestamps of the same counter (higher bits) are ordered by their server identifers (lower bits), e.g., \( 1.x \lt 1.y \lt 1.z \)
Miscellaneous #
- Why TaaS instead of
TrueTime?
- TaaS is designed to solve the problem within one data center. In contrast, TrueTime was intended for use across multiple data centers.